Konvolusi dengan metode tabular (komputational)

Proses konvolusi adalah proses menentukan sinyal output y[n] dari sebuah input tertentu x[n] dengan fungsi transfer tertentu h[n]. Konvolusi dapat memiliki input berupa sinyal kontinyu, maupun sinyal diskret. Deretan input x[n] ini berupa impuls satuan yang dilambangkan dengan δ[n]. Sedangkan deretan output berupa respon sistem deretan yang disimbolkan dengan h[n].
Proses konvolusi dapat definisikan (dilambangkan) dengan :

Dengan perubahan variabel, berlaku pula :

Kita sebut rumus diatas dengan rumus konvolusi. Fungsi transfer h[k] dari sebuah sinyal dikalikan dengan pencerminan sinyal dari sinyal input yang digeser sejauh n (x[n-k]).
Proses konvolusi dapat dilakukan dengan cara grafis/langsung (menggambar deretan sinyal input, transfer dan output), maupun dengan cara komputational (menggunakan perhitungan pada komputer). Kali ini akan dibahas tentang cara komputational.
Misal sinyal inputan x[n] dirumuskan dengan :

atau dapat ditulis dengan x[n]={2 , 4 , 0 , 1 , –2 , 3}. Tulisan yang tercetak tebal adalah nilai saat δ[n] = 0. Hal ini diperlukan untuk mengetahui pusat dari suatu deretan sinyal
dan transfer function h[n] dirumuskan dengan :

atau dapat ditulis dengan h[n]={2 , 0 , 1 , -2)
Kita diminta menentukan y[n] =x[n]*h[n]

CATATAN : Bila ingin mendapatkan gambar sesungguhnya, silahkan klik pada objek/gambar yang ingin dilihat.


1. Tuliskan x[k] dalam tabulasi
Deretan x[n] akan sama persis dengan deretan x[k]. Bila deretan x[k] dituliskan dalam tabulasi, maka dapat dituliskan seperti dalam gambar :

Pada gambar diatas, baris k adalah nomor deret dari sebuah sinyal diskret
Pada baris 2 diisikan x[n] yang dituliskan urut sesuai urutan pada k





2. Tuliskan h[n-k] dalam tabulasi
Konsep dari h[n-k] adalah ketika transfer function dari sebuah sistem dicerminkan dan digeser pada k. Sehingga deretan h[n-k] setelah dicerminkan adalah {-2 , 1 , 0 , 2}
Geser fungsi h[n] yang telah dicerminkan sehingga nilai terakhir pada deret h[n-k] sekolom dengan nilai pertama deret x[k]. Dalam hal ini, geser 2 (pada deret h[n-k]) untuk sekolom dengan 2 (pada deret x[k]).
Gambar sebelum h[n] dicerminkan dan digeser (Perhatikan baris h[n-k] dan posisi tiap bilangan pada kolom k !!!)

Gambar sesudah h[n] dicerminkan (Perhatikan baris h[n-k] !!!)

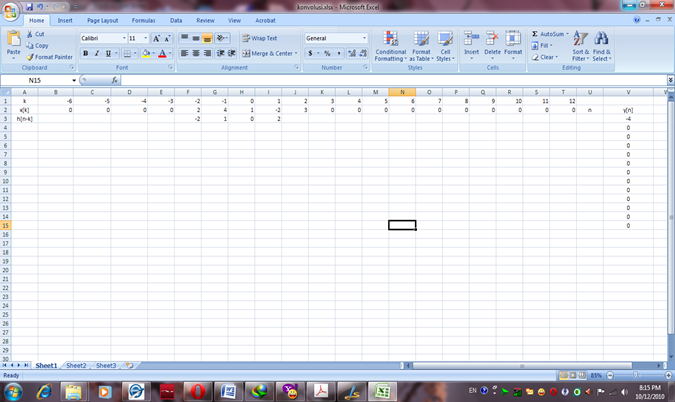
Gambar sesudah h[n] dicerminkan dan digeser (Perhatikan baris h[n-k] !!!)


3. Hitung jumlah total dari perkalian tiap kolom
Sesuai dengan rumus konvolusi, dimana

maka setiap deretan x[k] harus dikalikan dengan h[n-k]. Sehingga dari tabulasi dapat disajikan perhitungan (0 x –2) + (0 x 1) + (0 x 0) + (2 x 2) = 4

Gambar sesudah perhitungan dilakukan :


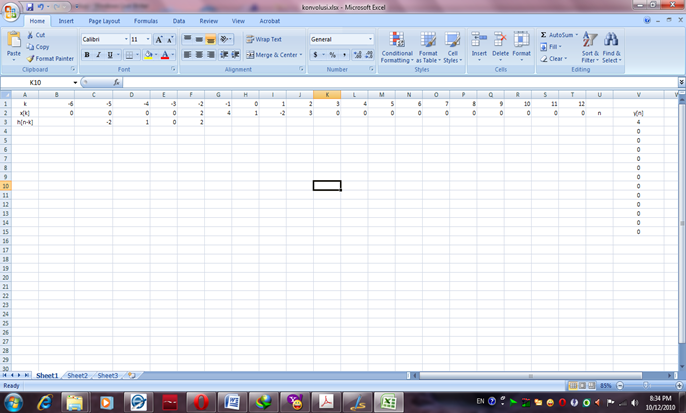
4. Menentukan kolom n
Permasalahan selanjutnya yang timbul adalah, bagaimana menentukan posisi/nomor deret dari suatu deretan output y[n]?
Seperti yang kita ketahui, bahwa dalam sebuah proses konvolusi input deret bilangan dengan transfer function yang juga berupa deret bilangan (impuls), maka proses konvolusi akan menghasilkan juga output berupa deret bilangan (deret impuls).
Penentuan kolom n ditentukan dari pada posisi k, dimana suatu deret h[n-k] berakhir. Mari kita lihat pada baris 3. Deretan h[n-k] dimulai pada sel C3 dan berakhir pada F3. Sedangkan nilai k pada sel F3 adalah –2 (sel F1). Sehingga nilai 4 dari perhitungan (0 x –2) + (0 x 1) + (0 x 0) + (2 x 2) berada pada deret –2 pada output y[n]


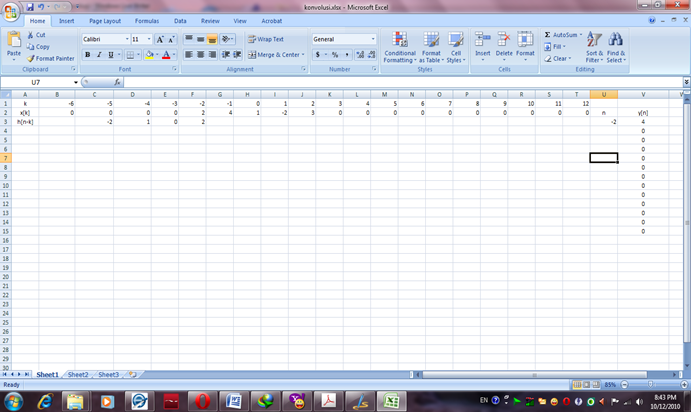
5. Geser h[n-k] maju sejauh 1 satuan pada kolom yang baru
Setelah ditentukan nilai pada y[n=2], maka sekarang kita menentukan y[n] untuk n yang lainnya. Caranya adalah dengan menggeser deretan h[n-k] maju 1 sel pada kolom yang baru.

gambar h[n-k] digeser 1 sel pada kolom yang baru (perhatikan pada baris 4!!!)


6. Menentukan nilai n pada h[n-k] yang telah digeser 1 sel
Penentuan nilai n pada h[n-k] yang telah digeser 1 sel akan sama dengan prosedur nomor 4

7. Menentukan semua nilai y[n] yang lain
Penentuan semua deretan output yang lain adalah dengan mengulangi prosedur nomor 3 sampai dengan 6
Gambar hasil dari proses konvolusi


Sehingga deretan y[n] = { 4 , 8 , 4 , –4 , –1 , –4 , 7 , –6 , 0 , 0 , 0 , 0 }
Dalam kasus tertentu, apabila y[n] menghasilkan deretan 0 yang tak terbatas, maka deretan tersebut dapat diabaikan. Sebagai contoh deretan y[n] diatas. Deretan setelah nilai –6 akan menghasilkan deretan 0 yang tak terbatas. Sehingga deretan tersebut dapat ditulis sebagai { 4 , 8 , 4 , –4 , –1 , –4 , 7 , –6 }.


By : Vincent E. Pradhana (2208100076)
Daftar Pustaka :
Proakis, John. G. 1996.  Digital Signal Processing : Principles, Algorithms, and Applications Third Edition. Prentice-Hall International, Inc. New Jersey.
Anonim. Diktat Pengolahan Sinyal Digital.