Suatu sinyal model apapun dapat dibawa dalam bentuk deret Fourier. Deret fourier mempermudah perhitungan untuk menghitung tiap nilai sinyal pada pias ke-n tertentu (n dalam bentuk integer). Deret Fourier atau Uraian Fourier merepresentasikan sinyal dalam bentuk deret sinus dan cosines. Deret Fourier didefinisikan sebagai :
didefinisikan pada selang
. Dimana koefisien Fourier
dan
adalah :
Bila didefinisikan pada selang sembarang, misal
yang memiliki periode
. Maka koefisien Fourier
dan
didefinisikan sebagai :
Suatu fungsi memiliki fungsi genap jika , dan fungsi ganjil jika
Contoh :
Grafik diatas adalah grafik. Bila ditulis dalam rumus syarat fungsi genap, maka :
Dari persamaan diatas dapat diambil kesimpulan bahwa fungsi adalah fungsi genap. Bandingkan dengan fungsi
Bila ditulis dalam rumus syarat fungsi genap, maka :
Kita coba menggunakan syarat fungsi ganjil :
Maka dapat diambil kesimpulan bahwa fungsi adalah fungsi ganjil. Terkadang suatu fungsi dapat tidak memenuhi syarat genap atau ganjil tersebut. Fungsi tersebut dinamakan fungsi tidak genap dan tidak ganjil. Dalam fungsi ganjil, hanya suku-suku sinus dan konstanta
yang dapat disajikan, sedangkan suku-suku cosines bernilai 0. Dalam fungsi genap, hanya suku-suku cosinus dapat disajikan, sedangkan suku
Contoh :
Tentukan Deret Fourier yang berkaitan!
Tentukan dulu komponen-komponennya, yaitu
Deret Fourier yang berkaitan adalah :
By Vincent E. Pradhana
(2208100076)
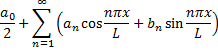





Tidak ada komentar:
Posting Komentar