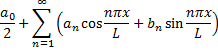Artificial Neural Networks

PERCEPTRON
Perceptron lapis tunggal adalah teknik jaringan saraf tiruan yang sangat sederhana. Teknik ini hanya mempunyai lapisan input, sebuah unit output dan terdapat bias(b), yaitu unit yang aktivasinya selalu 1 dan berperilaku sebagai layaknya bobot(w).
Algoritma yang dipakai adalah algoritma pelatihan, yaitu mengajarinya dengan contoh/pola sampai Jaringan saraf tiruan dapat mengenali pola tersebut. Seriap output yang dihasilkan tidak sesuai dengan target yang diharapkan, maka bobotnya terus di update sampai output sesuai dengan yang diharapkan. Bobot terakhir itulah yang akan digunakan saat pengaplikasian.
Algoritma perceptron adalah:
1. Masukkan input, dan nilai bias yang bernilai 1
2. Set aktivasi unit-unit input (xi), dengan nilai i=1,2,3,…,n
xi=si
3. Hitung respon unit output(y):
y=b+∑ xiwi
4. Maka, Nilai y=1 jika yin>0
Nilai y=0 jika y -0 Nilai y=-1 jika yin<0

post by Abdur Rahman 2208100181

KONVOLUSI

Metode lain untuk menganalisis system-sistem waktu diskrit didasarkan pada apa yang disebut barisan tenggapan-impuls dari sistem.
Rumus konvolusi adalah y=h*u
y[n] = ∑h[k]* x[n-k]
Secara umum pada system linear time invariant deretan output y[n] merupakan konvolusi diskrit “ ” antara deretan input x[n] dengan impuls respon sistem h[n].
Jadi y = x[n] * h[n]
Jumlah konvolusi tersusun dari empat operasi mendasar
1. Ambilkan bayangan cermin dari {h(n)} terhadap sumbu vertikal yang melalui titik asal untuk memperoleh {h(-n)}.
2. Geser {h(-n)} ke kanan sejauh suatu jumlah yang sama dengan nilai k dimana barisan keluaran dihitung, yang mana menghasilkan { h (k-n) }.
3. Perkalian barisan tergeserkan { h (k-n) } ini dengan barisan masukan { u(n)}.
4. Jumlahkan nilai-nilai hasil kali barisan ini untuk memperoleh nilai konvolusi di k.

Post by Abdur Rahman 2208100181

Deret Fourier

Suatu sinyal model apapun dapat dibawa dalam bentuk deret Fourier. Deret fourier mempermudah perhitungan untuk menghitung tiap nilai sinyal pada pias ke-n tertentu (n dalam bentuk integer). Deret Fourier atau Uraian Fourier merepresentasikan sinyal dalam bentuk deret sinus dan cosines. Deret Fourier didefinisikan sebagai :

didefinisikan pada selang . Dimana koefisien Fourier dan adalah :

Bila didefinisikan pada selang sembarang, misal yang memiliki periode . Maka koefisien Fourier dan didefinisikan sebagai :

Suatu fungsi memiliki fungsi genap jika , dan fungsi ganjil jika

Contoh :

Grafik diatas adalah grafik. Bila ditulis dalam rumus syarat fungsi genap, maka :

Dari persamaan diatas dapat diambil kesimpulan bahwa fungsi adalah fungsi genap. Bandingkan dengan fungsi

Bila ditulis dalam rumus syarat fungsi genap, maka :

Kita coba menggunakan syarat fungsi ganjil :

Maka dapat diambil kesimpulan bahwa fungsi adalah fungsi ganjil. Terkadang suatu fungsi dapat tidak memenuhi syarat genap atau ganjil tersebut. Fungsi tersebut dinamakan fungsi tidak genap dan tidak ganjil. Dalam fungsi ganjil, hanya suku-suku sinus dan konstanta yang dapat disajikan, sedangkan suku-suku cosines bernilai 0. Dalam fungsi genap, hanya suku-suku cosinus dapat disajikan, sedangkan suku

Contoh :

Tentukan Deret Fourier yang berkaitan!

Tentukan dulu komponen-komponennya, yaitu

             

jika

Deret Fourier yang berkaitan adalah :

 

By Vincent E. Pradhana

(2208100076)